A colleague of mine recently showed me his work on a novel approach to creating and rendering Constructive Solid Geometry (CSG) shapes: Instead of purely storing primitives in a CSG-operation tree and evaluating that at draw-time, the heavy lifting is offloaded to pointclouds - samples on the primitive surfaces, correctly clipped. In other words, nothing but a pointcloud has to be drawn, and rendering doesn’t scale with tree complexity or the amount or resolution of individual primitives.
In this post I won’t dwell on the pros and cons of this approach, nor the rendering side of things, but instead on the neat compute problems posed by implementing this algorithm on GPU and how I tackled them. The bird’s-eye view on what has to be done is simple:
- Take in new primitives and add/subtract them from the existing shape
- Compute and output new pointcloud
- Repeat
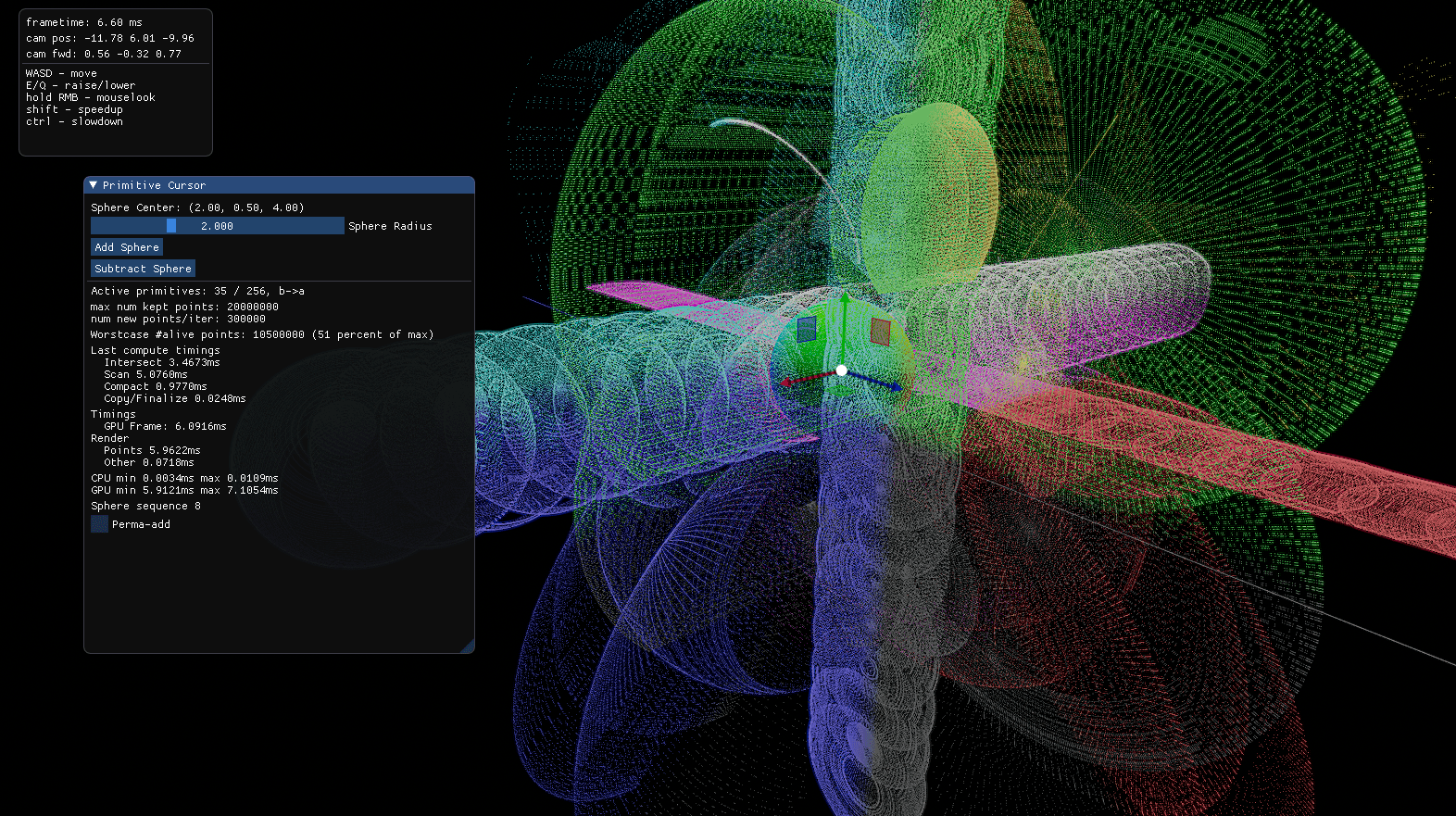
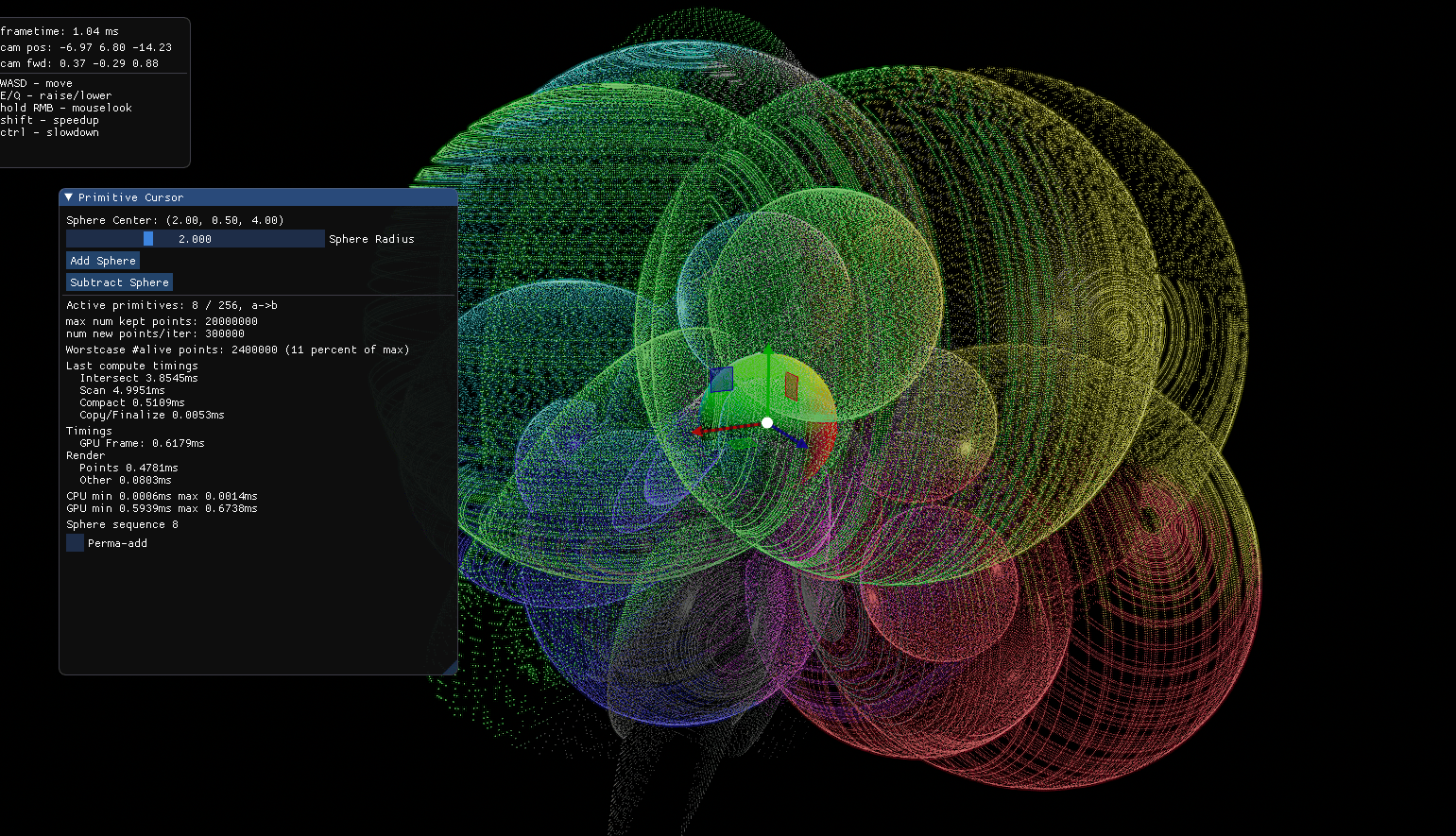
Sample rendering while randomly adding and subtracting spheres with the final algorithm
GPU Stream Compaction
Choosing a dimension of parallelization on GPUs is often straightforward: No thread creation overhead to take into account, scheduling is handled by dedicated hardware, simply go as wide as humanly possible. The obvious choice here is one thread per sample, especially since we’ll likely want lots of samples, on the order of multiple, maybe tens of millions.
My naive CPU implementation of the intersection test would certainly involve an array-append - we have new samples and conditionally add them to the persisted state. It would also require random erase, whenever old samples are removed by new subtract operations. While possible on GPUs (with atomics, HLSL’s AppendStructuredBuffer is ready to go right away), they are a poor match: All of our threads, in lock-step, would hit the same global atomic uint constantly, all but serializing the entire operation.
Luckily this problem is well understood in GPGPU, called stream compaction, and has a rather beautiful solution. First, each thread reads its element, evaluates a condition, and writes a keepflag to a parallel array - 0 or 1. Next, the prefix sum is calculated over the keepflag array - resulting in a second parallel array of unsigned integers. Finally, the original array is “compacted” - each thread reads its keepflag, and if 1, copies its element to the destination array, with the index given by the prefix sum.
Intersection Test
Given an array of CSG primitives in order, we can test a position against the combined shape as follows: Iterate the primitives in reverse and run the intersection tests. On the first hit, return true if the primitive was additive or false if it was subtractive. If none hit, return false. Note that there is a difference between “false - none hit” and “false - subtractive hit”, i’ll call the first one unaffected.
There are two fundamental modes for our intersection phase: A - old samples against new primitives, B - new samples against old primitives. A is simple: If an old sample intersects any new primitive, even an additive one, it is culled. This means a test result of !unaffected, being inside or outside doesn’t matter.
When culling new samples on the other hand, we have two subcases: B.1 - samples from an additive operation, B.2 - from a subtractive one. For B.1, samples are kept if unaffected or affected but outside of the CSG shape, this is intuitively clear. B.2 has these decisions exactly inverted - subtractive samples only appear whenever a preexisting shape is cut, to form the new hull of the CSG shape.

With the logic in place, it only has to get translated into an efficient kernel. We have two input arrays, the samples (huge) and the primitives (tens to hundreds), and one output array, the keepflags (one per sample). For now, my primitives are spheres, which simplifies the intersection test and only costs 4 floats per primitive: The center position and the squared radius, negative if the primitive is subtractive. This means 8 primitives fit on a 128B GPU L2 Cacheline. The problem is fundamentally bandwidth bound by the sample reads and keepflag writes, ideally the primitives are read from L2.
Im using a block size of 256 (, 1, 1) and a grid-stride loop for more flexibility and improved SM utilization, dispatching a set multiple of the amount of SMs on the current GPU. As im using the same shader for mode A and B, some control information is additionally passed in as root constants, packed into 16 bytes: The size of the input array, the amount of primitives, the dispatch size (X), the write offset into the output keepflag array, and the mode (A/B.1/B.2). Save for one little extra we’ll amend later on, that’s it for the intersection phase.
Parallel Scan
To compute the prefix sum, a parallel scan implementation must be chosen. Im using a standard two-phase up-sweep/down-sweep tree scan which is well illustrated in this GPU Gems chapter. To summarize, this algorithm allows us to calculate prefix sums per element on an array in one go, one thread per element. However, as shared memory is used, the array can only be as large as the thread block size, which is limited by hardware (ie. to 512 or 1024). As we want to operate on much larger arrays, we’ll have to use the “arbitrary size extensions” detailed in the chapter.
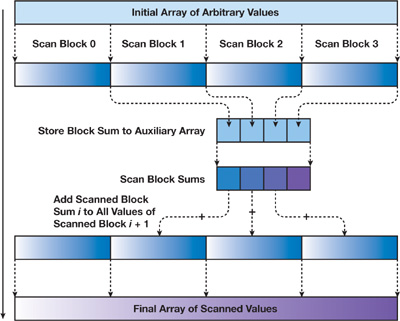
The large input array is locally scanned block-wise, meaning each block of 512 elements starts its prefix sum at 0 again. Then, the last element per block (the sum over all elements in that block) is in turn taken into a single “block sum” array. The block sum array is then scanned in one go. Finally, each element in the first block-wise scan is summed with its corresponding block sum scan to form the result. This works, but note that our new range is far from arbitrary: The inner block sum array must not be larger than a single thread block, meaning we can only support up to 512 blocks. Our new range has increased to just $512^2 = 262144$.
Since the goal is millions of samples, we’ll have to add one more level of hierarchy. Nothing changes about the first step, the wide array is still scanned block-wise. However, it is read into a level-one block sum array (length: $N / 512$) which is in turn scanned block-wise to form a level-two block sum array (length: $N / 512^2$). This one will finally be scanned in one go. Now, three instead of two intermediate arrays are summed into the result: The wide block-wise scan at current thread index, the level-one block sum scan at current group index, and the level-two block sum scan at (current group index / 512). If this was a little confusing, here’s the final sum in HLSL:
[numthreads(NUM_THREADS_PER_GROUP, 1, 1)]
void main_sum_results_two_level(uint3 group_id : SV_GroupID, uint3 thread_id : SV_DispatchThreadID)
{
uint l2_index = group_id.x / NUM_THREADS_PER_GROUP;
g_result[thread_id.x] = g_wide_scan[thread_id.x] + g_l1_scan[group_id.x] + g_l2_scan[l2_index];
}
With a total of four dispatches and three intermediate buffers, we have now achieved $$512^3 \approx 134 \text{M}$$ maximum elements, which is sufficient for now - this can be extended further with yet more layers.
Compaction
Most of the hard work is done by now, whats left is the compaction kernel. We have three array inputs: Uncompacted samples, keepflags, and the keepflag scan, and a single output array: The compacted samples. This kernel performs a conditional, redirected copy, probably fastest understood by taking a look at the code:
[numthreads(256, 1, 1)]
void main_compact(uint thread_id : SV_DispatchThreadID)
{
// grid-stride loop
int start_index = thread_id;
int stride = 256 * g_RootConsts.dispatch_size_x;
for (int i = start_index; i < g_RootConsts.num_samples; i += stride)
{
if (g_KeepFlags[g_RootConsts.keepflag_offset + i] != 0)
{
// the scan is inclusive, current value is one, thus subtract one to make it exclusive
uint dest_index = g_KeepFlagScan[g_RootConsts.keepflag_offset + i] - 1;
g_SamplesOut[dest_index] = g_SamplesUncompacted[i];
g_SampleParamsOut[dest_index] = g_SampleParamsUncompacted[i];
}
}
}
Note that so far, our samples have been nothing but positions, float3, yet they carry more data: Material parameters like a normal vector, albedo, metallic, roughness, what have you. Since we don’t want all that data to be uselessly taking up bandwidth during intersection tests, its kept in a parallel array and copied identically during compaction.
Just like intersection, we have two compaction dispatches, for the old and new samples each, differing in their input arrays and the keepflag offset.
Finalization and Integration
At this point, we have compacted samples, and sample parameters, ready to render - save for one thing: We don’t know how many to draw, at least not CPU side. Luckily the amount already exists on GPU memory, it’s simply the last element of the keepflag scan array. So to finish things up, we’ll copy that single uint to a separate GPU buffer containing an indirect draw argument (D3D12_DRAW_ARGUMENTS or VkDrawIndirectCommand respectively), and perform the drawcall using that buffer as an indirect argument. This indirect argument buffer will also be used in the A-phase intersect shader to discern live samples from dead ones, the written keepflag is always 0 if i >= g_IndirectArg.num_particles_alive.
We’ll also copy the newly uploaded primitives to the persisted primitive buffer so they’ll be available in the next iteration. This one is a straightforward concat, the amount of live primitives is always known on CPU.
Performance
At 256 primitives, 10M persisted samples, and 150K new ones per added primitive, performance on a RTX 2080 looks like this:
| Phase | Time (ms) |
|---|---|
| Intersect | 1.48 |
| Scan | 2.71 |
| Compact | 1.64 |
| Finalize | 0.006 |
| Total | 5.836 |
This amounts to about 1.7 billion samples per second and fits into a realtime setting quite well, taking data uploads and rendering into account - the samples are available for drawing right away.
Avoiding Padding
I was developing this demo on Vulkan and D3D12 in parallel and stumbled across some quite obvious alignment issues once I cut out the “alive” flag from my samples which left them at just a float3 position:
I wrote all shaders in HLSL and used DXCs SPIR-V path to feed Vulkan, which does not by default use “DirectX-style” data layouting for the SPIR-V path, and instead pads the float3 to 16 bytes. The quickest fix is of course explicitly padding the struct, both on HLSL and in C++, to 16 bytes with a single float _pad at the end. It might look innocent, but this has a signficant performance cost: Remember that both the intersect and compaction phase are bandwidth bound - thus increasing our data size by 33% almost directly translates to a performance degradation by the same factor:
| Phase | Time (ms) |
|---|---|
| Intersect | 2.14 |
| Scan | 2.67 |
| Compact | 2.04 |
| Finalize | 0.006 |
| Total | 6.856 |
(Note that the scan is unaffected as it doesn’t touch the samples.)
Luckily this can be fixed without compromising on performance or interoperability, using the -fvk-use-dx-layout DXC flag. Now both APIs use unpadded 12 byte-strided arrays.
Wrap up
With the barebones of this algorithm done, further development depends on usage. Some options to consider: Voxelizing the samples and primitives into chunks to cut down on intersection tests, optimizing the scan as it takes the most amount of time right now, using the compute queue asynchronously while rendering other parts of the scene, or pipelining sample drawing and computation, allowing a frame of latency.